 |
 |
|
|
RAY TRACING: NOTAS TECNICAS, TRUCOS, ALGORITMOS...Voy a agrupar en este página, y de manera provisional, pequeños trucos y técnicas sobre ray tracing y, más en general, sobre geometría computacional. Si el fichero crece lo suficiente, dividiré entonces la página, prepararé un índice, etc, etc.
ESTRUCTURAS DE DATOS PARA RAY TRACINGUno de los temas más importantes en ray tracing es el diseño de una estructura de datos apropiada que acelere el cálculo de intersecciones de rayos con objetos. Esta es un área que aún está abierta. Durante años, imperó la idea de que no se podía hacer mucho en este sentido, y la mayoría de los ray tracers utilizaban una estructura llamada Bounding Volumes Hierarchy (BHV), muy sencilla, pero poco eficaz. Ultimamente, la situación ha cambiado y se ha puesto de moda el uso de k-d trees para este propósito. El k-d tree es un árbol binario que, en cada nivel, divide el espacio de búsqueda mediante un plano. Su uso más conocido y original es almacenar puntos en un espacio multidimensional. No creo que finalmente sea la estructura de datos perfectas para el ray tracing, pero se puede adaptar para este propósito, y lo cierto es que parece dar buen resultado. De momento, XSight RT utiliza una variante modificada de BHV. La modificación consiste en que para acotar un grupo de objetos se pueden usar paralelepípedos alineados respecto a los ejes de coordenadas (el diseño clásico) o esferas contenedoras. La clave está en que es más eficiente intersectar un rayo con una esfera que hacerlo con un paralelepípedo: no es un resultado muy intuitivo que digamos, pero es fácilmente comprobable. El optimizador de escenas de XSight RT decide, para cada grupo de objetos, si es más eficiente acotarlos mediante un paralelepípedo o mediante una esfera.
HEURÍSTICAS BASADAS EN EL ÁREATanto si utilizamos un kd-tree o una BVH, el algoritmo que crea la estructura de datos recibe una lista de objetos geométricos. Esta lista se divide en dos fragmentos que se enlazan mediante un nodo arbóreo, y la división continúa de forma recursiva en los nuevos nodos creados. ¿Qué criterio se utiliza para dividir una lista de objetos en dos subconjuntos? La técnica tradicional se parecía a la siguiente:
La siguiente imagen muestra en qué situación nos encontraremos al llegar a esta parte del algoritmo: 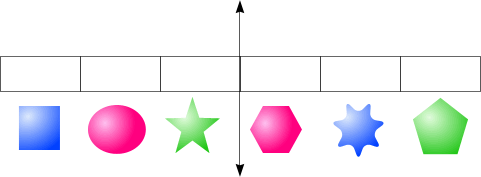 Hasta hace muy poco, la recomendación era dividir la lista en dos partes con el mismo número de objetos, o alternativamente, elegir como punto de fractura aquel que estuviese más cercano al centro del intervalo definido por la lista de objetos. No obstante, existe un criterio mucho mejor para la división. La técnica consiste en minimizar el valor de esta expresión: 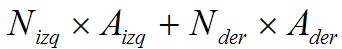 Es decir: se multiplica el número de objetos que quedarían en el nodo izquierdo por el área total del volumen que encerraría a dichos objetos, y se suma a la expresión correspondiente aplicada al nodo de la derecha. Muy importante: en realidad, no nos interesa el volumen total a la derecha y a la izquierda... ¡sino el área de dicho volumen! La explicación es sencilla: la posibilidad de que un rayo aleatorio intersecte un objeto arbitrario es proporcional al área de dicho objeto. Algunas observaciones:
INTERFAZ DE PROGRAMACIÓN DE OBJETOS GEOMÉTRICOSLas clases que implementan objetos geométricos en XSight RT se caracterizan por implementar el tipo de interfaz IShape. ¿Qué funcionalidad mínima debe ofrecer una interfaz del tipo IShape? En ray tracing, existen dos escenarios diferentes para la intersección de rayos y objetos de una escena. Normalmente, bastaría con que IShape definiese un solo método: public interface IShape
{
bool HitTest(Ray ray, Double maxDistance, ref HitInfo info);
}HitTest debe averiguar si un rayo determinado tropieza en su avance con el objeto en cuestión, y en caso afirmativo, debe ofrecer información sobre dicha intersección:
He dicho que basta con el método HitTest, pero existe un caso especial de intersecciones que nos interesa tratar y optimizar por separado. Existen dos tipos fundamentales de intersecciones entre rayos y objetos:
Como ve, la diferencia fundamental consiste en que, en el segundo caso, podemos terminar el algoritmo en cuanto tropezamos con una intersección, y en el segundo caso, nos interesa comprobar si existe una intersección más cercana. Para poder tratar ambos casos por separado, se añade un segundo método a IShape: public interface IShape
{
bool HitTest(Ray ray, Double maxDistance, ref HitInfo info);
bool ShadowTest(Ray ray);
}Ya no pasamos la distancia máxima a ShadowTest... porque asumimos que siempre será 1.0. Esto sucede gracias a que la longitud del vector de dirección coincide con la distancia a la fuente de luz. Además, no nos interesa conocer los detalles sobre la intersección, por lo que ahorramos algo no pasando el parámetro de tipo HitInfo. Con algunas pequeñas adiciones, ésta era la definición de IShape en las primeras versiones de XSight RT, cuando todavía no permitíamos crear nuevas figuras geométricas mediante intersecciones y diferencias de volúmenes. La siguiente imagen muestra el resultado de intersectar un paralelepípedo con un cilindro, para luego eliminar una franja rectangular del resultado (una intersección seguida de una diferencia):  Estas operaciones se implementan en ray tracing mediante los llamados diagramas de Roth. Para empezar, tenemos que conocer de antemano todas las intersecciones entre un rayo y un objeto determinado. Suponga que en una escena hemos situado el objeto resultante de una diferencia entre un cubo y un cilindro vertical. Comenzamos averiguando en qué momento el rayo de la cámara tropieza con las paredes de ambos objetos: 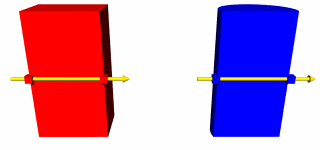 Mezclamos entonces los tiempos obtenidos en una misma lista ordenada:  La diferencia entre dos sólidos es el conjunto de puntos que pertenecen al primero, pero no al segundo. Lo que hacemos a continuación es llevar la cuenta de cuándo estamos dentro del primer objeto y cuándo estamos dentro del segundo. Lo primero cambiará cada vez que tropecemos con uno de los puntos marcados para el primer objeto, y lo mismo ocurrirá con lo segundo. En este caso particular, los cuatro puntos encontrados también marcarán las fronteras (respecto al rayo utilizado) del objeto resultante: 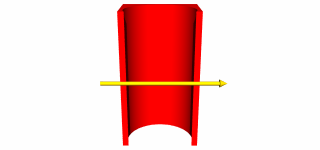 Para que un objeto geométrico pueda participar en este tipo de algoritmos, necesitamos nuevos métodos para IShape: public interface IShape
{
bool HitTest(Ray ray, Double maxDistance, ref HitInfo info);
bool ShadowTest(Ray ray);
int MaxHits { get; }
int GetHits(Ray ray, Hit[] hits);
Vector GetNormal(Vector location);
}El primero de los métodos (en realidad, se trata de una propiedad) se llama solamente durante la inicialización de la escena, y nos dice el número máximo de veces en el que un rayo arbitrario puede cruzarse con las fronteras de una figura determinada. Para cualquier objeto convexo, como las esferas, cubos y cilindros, hay un máximo de dos intersecciones. Un toro o rosquilla admite hasta cuatro intersecciones, y por ello no se considera un sólido convexo. Esta información se utiliza para configurar las listas antes de iniciar la generación de la imagen. El plato fuerte, no obstante, es GetHits, que dado un rayo, debe copiar todos los puntos de intersección con el mismo en una lista (el parámetro hits). Como valor de retorno, se devuelve el número de intersecciones realmente encontradas. Observe que esta vez no hay una cota máxima para la distancia... ¡y tampoco una cota mínima! Finalmente, necesitamos un método que, dado un punto en la superficie de un objeto, nos devuelva el vector normal a la superficie en dicho punto. Esa información podría pasarse en la misma lista hits donde ponemos los puntos de intersección, pero eso nos obligaría a calcular muchos vectores normales que al final no serían necesarios. Observe también que he utilizado un segundo tipo de estructura, Hit, en vez del tipo HitInfo usado para el algoritmo de intersección más habitual.
DUALIDAD GEOMÉTRICAEsto no es un "truco", ni un algoritmo, hablando con propiedad, sino una técnica procedente de la Geometría Proyectiva, que se utiliza mucho en Geometría Computacional. Voy a presentar una forma muy particular de la misma. Si quiere averiguar sobre una forma más general, busque información sobre coordenadas homogéneas. Vamos a limitarnos, para simplificar, a la geometría planar, en dos dimensiones. En un plano existe una relación dual entre puntos y líneas, que definiremos del siguiente modo:
De este modo, se cumplen las siguientes propiedades:
Veamos ahora cómo aplicar este conocimiento. Una línea sobre un plano divide siempre a este plano en dos mitades. Esto se puede aprovecha para definir polígonos convexos como la intersección de una lista de semiplanos definidos mediante líneas. De hecho, la forma más simple de definir un poliedro en ray tracing consiste en intersectar los semiespacios definidos por un conjunto de planos: la misma técnica, pero extrapolada a tres dimensiones. Suponga que definimos un polígono mediante cuatro líneas. En la siguiente imagen, estamos hablando de las líneas dibujadas en azul: 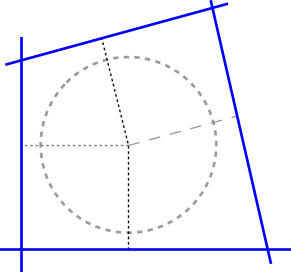 El caso es que cada una de las líneas azules va asociada a un punto dual. Para simplificar, he asumido que el origen de coordenadas está dentro del polígono azul, y que las cuatro líneas son exteriores a un círculo con radio unitario. En este caso, los cuatro puntos duales caerán en el interior de este círculo. Podemos unir estos cuatro puntos para obtener el polígono dual, que he dibujado con líneas rojas: 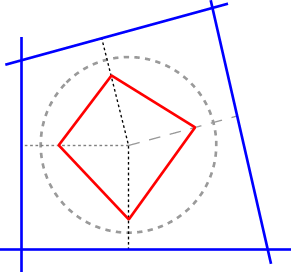 ¿Y ahora qué? Bien, suponga que añadimos una quinta línea en la definición del polígono azul. Puede ser que esta nueva línea "recorte" una o más esquinas del polígono ya existente, definiendo una nueva figura... o puede que la nueva línea nunca tropiece con el polígono. En este segundo caso, se trataría de una línea que define un semiplano redundante. Podríamos eliminar la nueva línea de la definición. Podría ocurrir también que la nueva línea no sea redundante, pero que convierta en redundante a otra línea ya existente en la definición. Si dibujásemos la línea, nuestra intuición geométrica nos indicaría casi inmediatamente en qué caso nos encontramos. Pero si sólo disponemos de los datos análiticos de la línea, ¿cómo se puede determinar si la línea es o no redundante? La respuesta es sorprendentemente simple: calcule el punto dual a la nueva línea. Si el punto dual se encuentra en el interior del polígono dual, la línea es redundante. Si se encuentra fuera, la línea define un nuevo polígono. Me perdonará que no incluya la demostración del teorema. Intuitivamente, sin embargo, es fácil ver el motivo: mientras más lejos esté la línea del origen, más cercano a éste estará su punto dual, ¿recuerda? ¿Y qué aplicación puede tener esto en ray tracing? Como he dicho antes, podemos definir poliedros intersectando planos (más exactamente, los semiespacios que estos delimitan). Por ejemplo:
La técnica es sencilla, pero tiene un inconveniente: hay que encontrar un volumen que incluya al poliedro en su interior. Unos cuantos programas de esta clase fuerzan al diseñador a suministrar manualmente el volumen contenedor, con todo el riesgo y el esfuerzo innecesario que esto ocasiona. XSight RT, por el contrario, calcula este volumen. Para ello, debe encontrar los vértices del poliedro resultante a partir de los datos sobre los planos que lo definen. ¿Cómo hacerlo? ¿Empezamos a resolver ecuaciones lineales en plan bestia? Hay una técnica mejor: para cada plano, calculamos el punto dual correspondiente. Una vez que tenemos el conjunto de puntos duales, utilizamos un algoritmo muy sencillo y popular para calcular la cápsula convexa (convex hull) que encierra todos estos puntos. Es decir, transformamos el problema de encontrar los vértices de un poliedro en el cálculo de los vértices de otro poliedro... sólo que esta vez, existe un algoritmo sencillo y muy conocido para esta tarea. Y una vez que tenemos el poliedro dual, ¿cómo demonios obtenemos los vértices que realmente estábamos buscando? Muy sencillo: ¡las caras o facetas del poliedro dual se corresponden por dualidad a los vértices del poliedro original! Volvamos al diagrama en el plano: 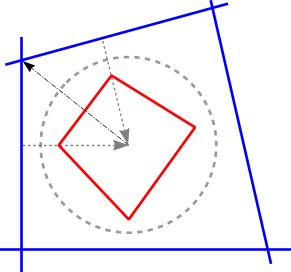 A las líneas azules, por dualidad, le corresponden los puntos de un polígono dual. Recíprocamente, el lado que corresponde a los dos puntos duales se transforma, también por dualidad, en el vértice asociado a la intersección de las dos líneas originales. Recuerde, no obstante, que el caso explicado aquí es aquel en el que el origen de coordenadas está contenido dentro del polígono o poliedro. La técnica se puede extender, por supuesto, al caso más general.
INTERSECCION ENTRE RAYOS Y ESFERASEl núcleo del ray tracing son las rutinas que calculan las intersecciones entre un rayo y los distintos objetos geométricos que se permitirán en las escenas. Cualquier pequeña optimización en este apartado, merece la pena, pues se hace notar en el rendimiento de manera casi automática. Sorprendentemente, de todos los objetos tradicionales usados en ray tracing, es la esfera la que tiene un algoritmo de intersección más eficiente. Voy a mostrarle, primero, cómo se deduce la fórmula para las intersecciones a partir de la propia definición de la esfera. Luego, veremos cómo se traduce la fórmula en código C#. Primero, veamos cómo definiremos nuestras esferas: 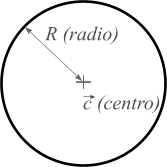 Se trata de un diagrama plano, pero es fácil extrapolarlo a tres dimensiones. Como puede ver, la esfera se define indicando las coordenadas del centro y el radio. Utilizaré el convenio de destacar los vectores colocando una flecha encima del símbolo. En este caso, el centro de la esfera es un vector, y el radio, un valor escalar. Cuando haga referencia a un vector en el texto, por el contrario, usaré negritas. Para que un punto r arbitrario se encuentre en la superficie de la esfera, debe satisfacer esta igualdad: 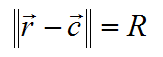 Los palitroques dobles significan la longitud del vector encerrado en su interior, y el significado de la ecuación es casi trivial: la distancia entre los puntos de la superficie de la esfera y el centro de la misma debe ser igual al radio de la esfera. La longitud de un vector se define de esta manera: 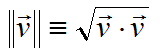 En el lado derecho de la ecuación, multiplicamos el vector consigo mismo y luego hallamos la raíz cuadrada del resultado. La "multiplicación" que se utiliza es el llamado producto escalar de vectores: el producto escalar de un vector(a, b, c) con otro vector (d, e, f) es el número a * d + b * e + c * f. Si se trata de calcular el producto escalar del vector (x, y, z) consigo mismo, el resultado es x * x + y * y + z * z. Para calcular la distancia, se necesita calcular una raíz cuadrada. Podemos eliminar esta raíz si, en la definición de la esfera, elevamos al cuadrado cada una de las partes: 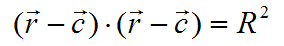 Ahora bien, lo que queremos encontrar son los puntos que estén, a la misma vez, en la superficie de la esfera, y en un rayo determinado. La ecuación vectorial que define un rayo es la siguiente: 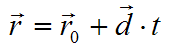 El vector r0 es el origen del rayo, y el vector d es la dirección del rayo. El símbolo escalar t representa el parámetro tiempo: variando el valor de t, podemos obtener todos los puntos que conforman el rayo. El siguiente paso es el más importante de todos: mezclaremos las dos definiciones. Si un punto pertenece tanto a la esfera como al rayo, tiene que satisfacer ambas condiciones. Si sustituímos el vector r de la definición de la esfera por la ecuación del rayo, obtendremos lo siguiente:  Nuestra meta es despejar la t en la ecuación anterior, para lo cual tendremos que librarnos de toda la chatarra vectorial. Podemos, por ejemplo, simplificar un poco la ecuación haciendo la siguiente sustitución: 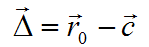 Esta es la ecuación tras la sustitución: 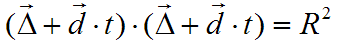 Podemos aplicar las reglas de distributividad y asociatividad al lado izquierdo, para transformar la ecuación de esta manera: 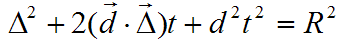 Observe que he aplicado otro convenio notacional: cuando multiplicamos un vector consigo mismo, podemos indicarlo también elevando el símbolo al cuadrado. Por ejemplo: 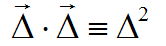 Lo importante es que ahora es fácil reconocer una ecuación de segundo grado en nuestra ecuación. Echando mano de la popular fórmula de resolución, obtenemos esta fórmula para calcular los dos posibles instantes t en los que el rayo puede tropezar con la superficie de la esfera: 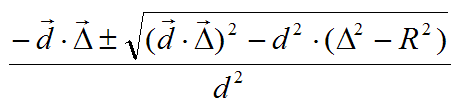 Todos los valores en esta fórmula final son conocidos: el símbolo delta es el resultado de restar el centro de la esfera del origen del rayo, d es la dirección del rayo, y R es el radio de la esfera. Si la expresión encerrada dentro de la raíz cuadrada (técnicamente hablando, el discriminante) es negativa, el rayo no se cruza con la esfera. Si el discriminante es cero, el rayo roza la esfera en un solo punto. De lo contrario, el rayo entra por un lado de la esfera y sale por el otro. Con la fórmula anterior, es muy sencillo programar las pruebas de intersección de una esfera. El siguiente fragmento de código muestra los detalles más importantes: public struct Vector
{
public double X, Y, Z;
}
public class Ray
{
public Vector Origin, Direction;
}public sealed class Sphere : MaterialShape, IShape
{
private Vector center;
private double radius, radius2;
// ...
}bool IShape.ShadowTest(Ray ray)
{
double x = center.X - ray.Origin.X;
double y = center.Y - ray.Origin.Y;
double z = center.Z - ray.Origin.Z;
double ray2 = 1.0 / ray.Direction.Squared;
double beta = ray2 *
(x * ray.Direction.X + y * ray.Direction.Y + z * ray.Direction.Z);
double discr = beta * beta - (x * x + y * y + z * z - radius2) * ray2;
if (discr < 0.0)
return false;
discr = Math.Sqrt(discr);
double t = beta - discr;
if (t < Tolerance.Epsilon)
{
t = beta + discr;
if (t < Tolerance.Epsilon)
return false;
}
return t <= 1.0;
}En realidad, sólo he mostrado la implementación de ShadowTest, el método que comprueba las intersecciones de los rayos de sombra, por ser la más independiente de otros módulos del ray tracer. Observe que no se utiliza un operador para los varios productos escalares de vectores: estoy mostrando código "real", y los operadores del CLR exigen que sus parámetros se pasen por valor, lo cual es muy ineficiente para tipos de valor como Vector, que ocupa unos 24 bytes. Naturalmente, la mayor eficiencia tiene un precio: el código es menos legible. Una solución a esto sería la traducción en línea del propio código IL, como la implementa Delphi.NET, pero no C# o Freya, al menos de momento (está dentro de los planes de Freya).
VECTORES NORMALESLa parte más complicada al añadir una nueva primitiva geométrica a un ray tracer es, por supuesto, el cálculo de las intersecciones entre la primitiva y los rayos. Pero hay una segunda tarea, que aunque más sencilla, también puede complicarse: el cálculo del vector normal a la superficie, dado el punto de intersección entre la primitiva y el rayo. He comprobado que muchas de las fórmulas que flotan por Internet para calcular normales tienen errores. Sin embargo, es relativamente sencillo generar la fórmula correcta. Hay dos fórmulas matemáticas alternativas, que se pueden utilizar para calcular el vector normal. La técnica a elegir depende de la forma en que se defina la superficie:
Una superficie implícita se define como los puntos del espacio que satisfacen una ecuación de este tipo: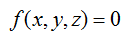  
Supongamos, por ejemplo, que estamos definiendo una esfera de cuarto grado, como las que recientemente hemos añadido a XSight RT: 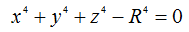 La fórmula de la normal para superficies implícitas es extraordinariamente sencilla: 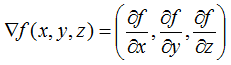 Se trata, efectivamente, del gradiente de la función utilizada en la definición. En el caso de la esfera de cuarto grado, el gradiente de la función es: 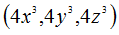 Hay que tener sumo cuidado con dos detalles. El primero es la longitud del vector normal, pues en la mayoría de los casos, el ray tracer espera normales unitarias, de longitud uno. En nuestro ejemplo, eliminaríamos el factor constante de la expresión del gradiente, luego calcularíamos la longitud del vector y "normalizaríamos la normal" (valga la redundancia). El segundo detalle tiene que ver con la dirección del vector. Técnicamente hablando, la normal podría apuntar tanto hacia "fuera" como hacia "dentro": recuerde que se trata de una superficie, y que no todas las superficies delimitan un volumen finito, por lo que no tiene siempre sentido hablar de "fuera" y "dentro". En nuestro caso, sin embargo, la elección es evidente: queremos que el vector normal se aleje del centro de coordenadas. Una superficie puede definirse también mediante un conjunto de puntos determinados por dos parámetros: 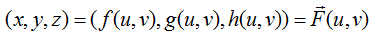 La derivada parcial respecto a cualquiera de los dos parámetros se interpreta como una de las tangentes a la superficie. Está claro que el vector normal debe ser perpendicular a todas las tangentes, por lo que es posible obtenerlo mediante el producto vectorial de las dos derivadas parciales: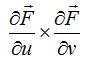 
|
intersection(
plane(-^z, 1, m) spin [+52.6625, 0, 0],
plane(-^z, 1, m) spin [+52.6625, 72, 0],
plane(-^z, 1, m) spin [+52.6625, 144, 0],
plane(-^z, 1, m) spin [+52.6625, 216, 0],
plane(-^z, 1, m) spin [+52.6625, 288, 0],
plane(-^z, 1, m) spin [+10.8125, 0, 0],
plane(-^z, 1, m) spin [+10.8125, 72, 0],
plane(-^z, 1, m) spin [+10.8125, 144, 0],
plane(-^z, 1, m) spin [+10.8125, 216, 0],
plane(-^z, 1, m) spin [+10.8125, 288, 0],
plane(-^z, 1, m) spin [-52.6625, 36, 0],
plane(-^z, 1, m) spin [-52.6625, 108, 0],
plane(-^z, 1, m) spin [-52.6625, 180, 0],
plane(-^z, 1, m) spin [-52.6625, 252, 0],
plane(-^z, 1, m) spin [-52.6625, 324, 0],
plane(-^z, 1, m) spin [-10.8125, 36, 0],
plane(-^z, 1, m) spin [-10.8125, 108, 0],
plane(-^z, 1, m) spin [-10.8125, 180, 0],
plane(-^z, 1, m) spin [-10.8125, 252, 0],
plane(-^z, 1, m) spin [-10.8125, 324, 0]);