Splines

Splines are piecewise defined functions, using cubic polynomials, for interpolating or smoothing curves. Austra can create splines for time series, using dates as arguments, or for any pair of vectors containing abscissas and coordinates, respectively. There is also a shortcut for creating this second kind of splines given a grid on an interval and an arbitrary function.

All spline kinds are created using overloaded variants of the same class method:

This example shows how to create and use a spline based on a time series:

let s = spline(appl) in
    s[appl.last.date - 15]

The example creates a spline based on the series values, and then the spline is used to interpolate the value fifteen days before the last date stored in the series.

At a first glance, it may seem than interpolating a daily series does not make sense, since AUSTRA dates do not include a time fraction. Nevertheless:

• Even daily series have gaps corresponding to holidays.
• You can still use a real value for interpolating a spline with date arguments.

The following formula, for example, finds what would be the value at a middle time between two consecutive dates:

let s = spline(appl) let
    s[4@jul20.toInt + 0.5]

We are adding half of a day, i.e., twelve hours, to the numerical equivalent of a date, if the stored values in the time series corresponds to each day’s midnight.

Splines can also be used to interpolate existing data and functions:

-- Use a function over a uniform grid.
let s1 = spline(0, τ, 1024, cos);
s1[π/4] - sqrt(0.5);
s1.derivative(π/4);
-- Use two arbitrary vectors with the same length.
let s2 = spline([1, 3, 4, 5], [0, 1, 0.8, 0]);
s2[2]

Indexers, methods and properties

All splines have these four properties:

For instance, we can use it to approximate the area below a normal distribution:

-- The integral over a reasonable interval.
spline(-10, 10, 10000, x => exp(-x²)).area;
-- The expected result.
sqrt(π)

These are the methods implemented by splines:

The poly method has two overloads: one receives an integer, and the other allows a C# Index as its argument:

-- Let’s define a spline with a function over a uniform grid.
let s1 = spline(0, τ, 1024, cos);
-- Retrieve the polynomial for the first segment of the spline.
s1.poly(0);
-- Two alternatives for retrieving the last polynomial:
s1.poly(s1.length - 1);
s1.poly(^1);

Polynomials retrieved with the poly method accepts values in the closed interval [0,1]. The spline interpolator must find the polynomial, subtract the initial argument for the corresponding segment and scale the remaining offset according to the length covered by the segment.

Each polynomial provides two methods, for evaluating its value and its derivative at a point in the closed interval [0,1], and one property, area, for evaluating the definitive interval of the polynomial over its valid interval:

Interacting with a spline

When a spline is evaluated in the Austra Desktop application, an interactive control is shown. You can enter values in the Argument text box to evaluate the spline and its derivative at the supplied argument. This control appears no matter which argument type is being used for the spline:

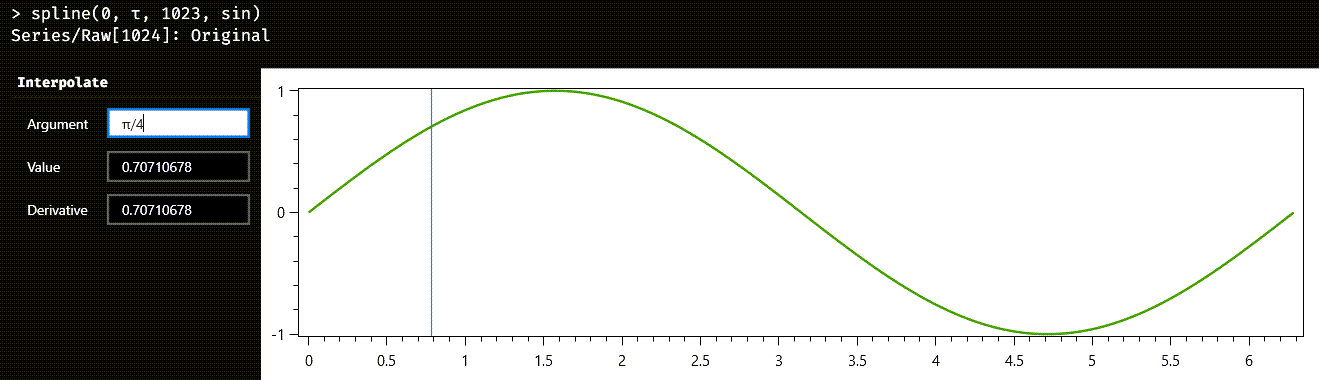
For numeric arguments, you can even type an Austra formula in the text box, and Austra evaluates the formula when Enter is pressed.

Reference

Other Resources